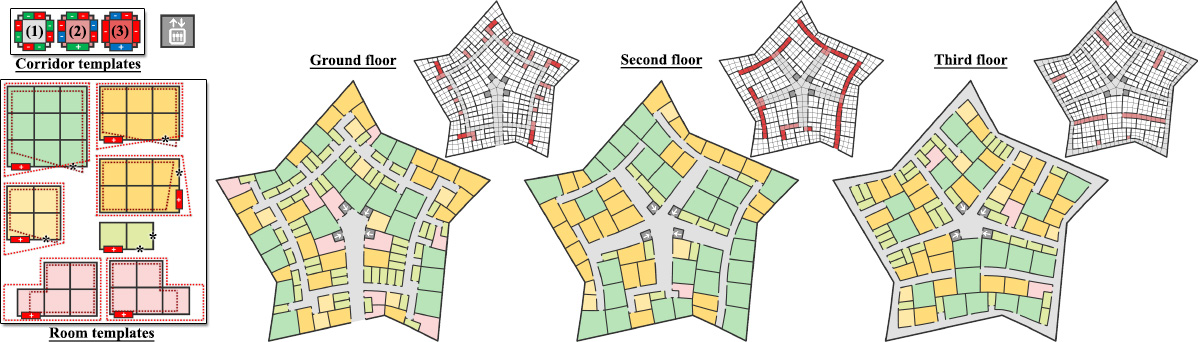
Our framework is able to generate layouts that meet both accessibility and aesthetic criteria for arbitrarily shaped (e.g., non-axis aligned) domains. Here, we show several floorplan layouts for a pentagon-shaped building. The accessibility criteria specify that all rooms are connected to the elevators via a singly connected corridor. The aesthetic criteria specify the admissible deformations for the rooms. Upper-left: A set of tile templates to build the corridor: (1) predefined locations of the corridor, (2) first-level branches of the corridor, and (3) second-level branches of the corridor. Observe how these topological constraints are enforced by the the edge-color constraints of the tiles. Bottom-left: A set of deformable room templates. The doors are constrained to be at the edges with red colors (alternative locations are marked with a star). Certain rooms are deformable to be quads with two right angles. Right: We show three distinct floorplan designs for different floors of the building. The different designs are achieved by different predefined locations of the corridor (grey parts in the sub-figures in the upper-right corners). The corridor branches and the rooms are then found by our discrete tiling algorithm in a way such that rooms are placed with a higher priority. Finally, the mesh geometry is optimized to minimize the deviations of the rooms from their admissible shapes and the straightness of the room boundaries.

---

Abstract

In this paper, we tackle the problem of tiling a domain with a set of deformable templates. A valid solution to this problem completely covers the domain with templates such that the templates do not overlap. We generalize existing specialized solutions and formulate a general layout problem by modeling important constraints and admissible template deformations. Our main idea for the solution is to break the layout algorithm into two steps: a discrete step to lay out the approximate template positions and a continuous step to refine the template shapes. Our approach is suitable for a large class of applications, including floorplans, urban layouts, and arts and design.

---

Framework Overview

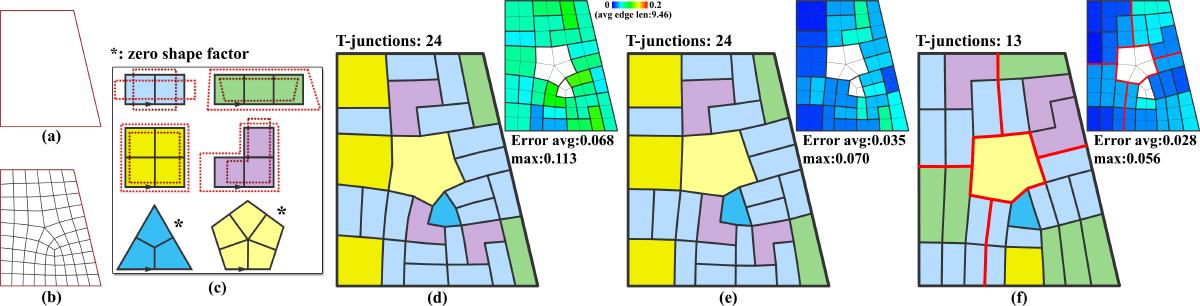
Overview of our framework. (a) and (b) The problem domain and its quadrangulation. (c) The given tile templates. Each template is shown as its base polygon and its admissible transformations (upper left: rectangles with arbitrary ratios of side lengths, upper right: trapezoids with parallel top and bottom sides, middle left: squares, middle right: J-shaped tiles with arbitrary ratios of lengths of the two ends, bottom left and right: these triangle and pentagon tiles can be arbitrarily transformed. Arrows denote the anchors. (d) A complete tiling with a small average shape registration error is generated by linear integer (Boolean) programming with shape factors included in the weighting scheme. Note that the shapes of the triangle and pentagon tiles are irrelevant (zero shape factors). The shape registration errors are visualized in the upper-right corners. (e) The mesh geometry is optimized to further reduce the shape registration errors. (f) A custom tiling design with user-specified tile boundary constraints (red lines) and regular-junction constraints added to reduce the number of T-junctions.

---

Results and Applications

(1) Floorplan

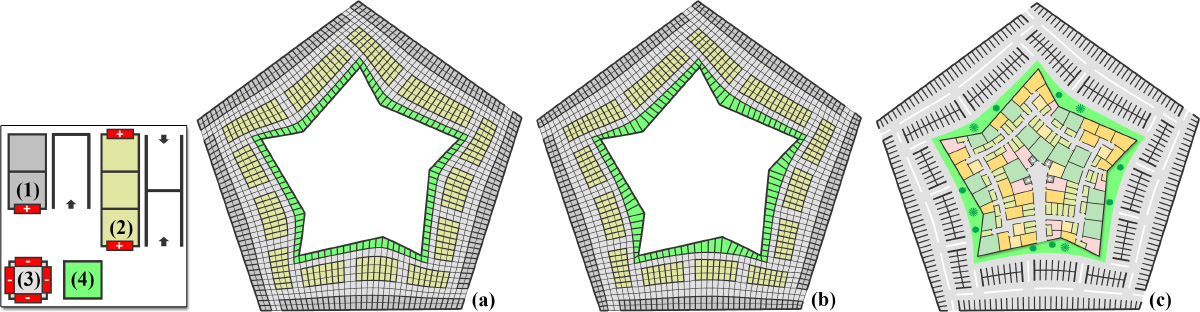
Top and bottom rows: two floorplan examples using the same corridor and room templates in the first figure.

Parking lot design using a set of templates with edge color constraints to enforce the accessibility criteria: (1) and (2): templates for a full-sized and a twin compact-sized parking lot. Edges that must access roads are given the positive red color. (3) Road tiles of which every edge is given a negative red color for parking lot access. (4) Green tiles with flexible shapes. (a) and (b): The tiling before and after a geometric optimization. Road tiles are specified by the user. We allow only similarity transformations for the parking lot and road tiles. However, the concave spaces that were difficult to use are accommodated by the green tiles with flexible shapes. (c) A stylization of the tiling obtained by manually adding trees and replacing tiles by (warped) 2D vector textures.

(2) Urban Pattern Layout

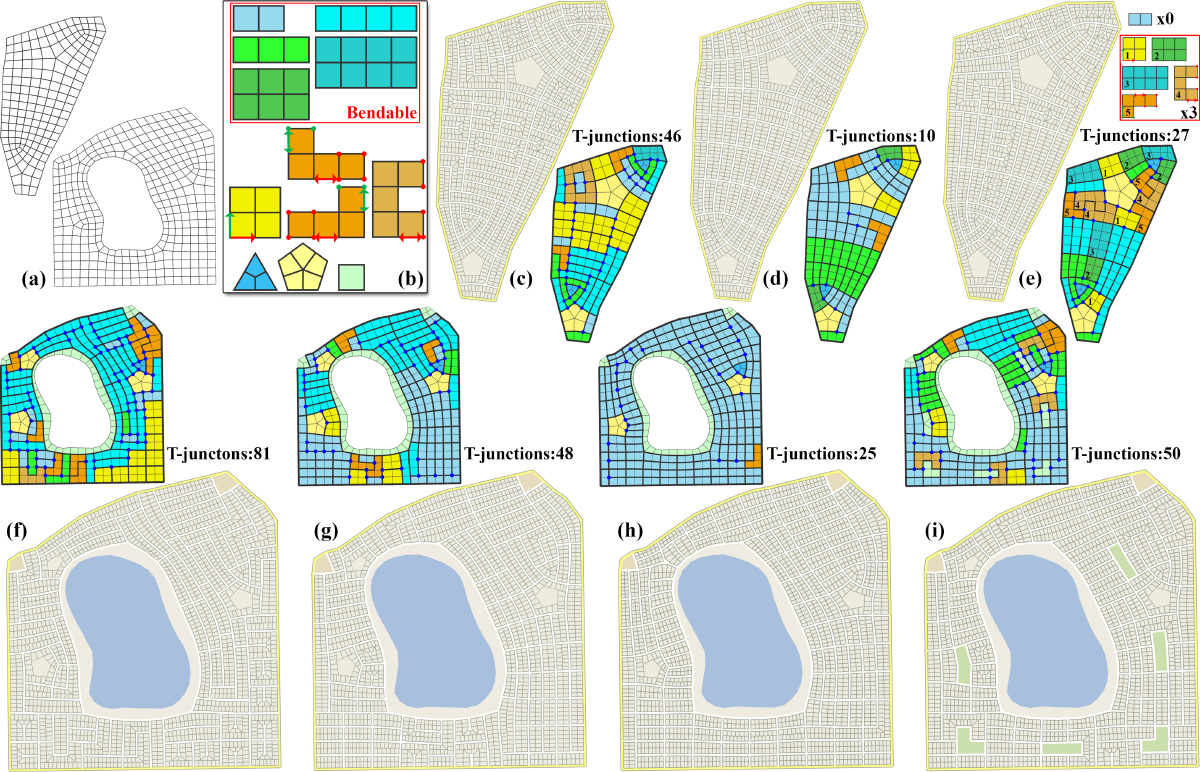
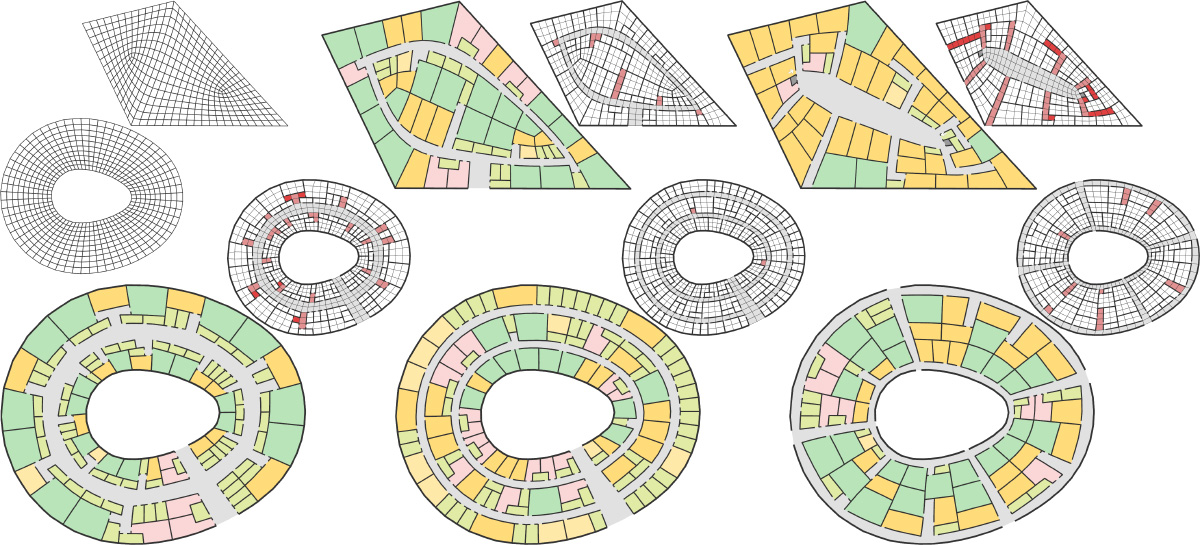
Urban layout design. (a) The quadrangulations of two problem domains from [Yang et al. 2013]. (b) We create a set of tile templates that includes more general tiles as can be handled by Yang et al.: 1) a set of bendable tiles, 2) L-shaped, J-shaped, and U-shaped tiles of which each end can stretch individually, 3) 2x2 square tiles that can scale non-uniformly, 4) triangle-shaped and pentagon-shaped tiles that can only scale uniformly, and 5) single-quad tiles with lower weights for shape optimization (these tiles are used to model lake shores and parks with flexible shapes). Each tile may take a further similarity registration. (c) to (e): Three different designs for the first problem domain. We can create layouts that favor variety (c) and regularity (d), i.e., fewer numbers of T-junctions, by controlling the weights for the regular-junction constraints. (e) We can precisely control the numbers of occurrences for each tile template. (f) to (i): Four different designs for the second problem domain. (f) to (h): Designs with increasing regularity, at the cost of decreasing variety. The second one (g) is a nice example that strikes a balance. (i) A design with user-specified locations of parks.

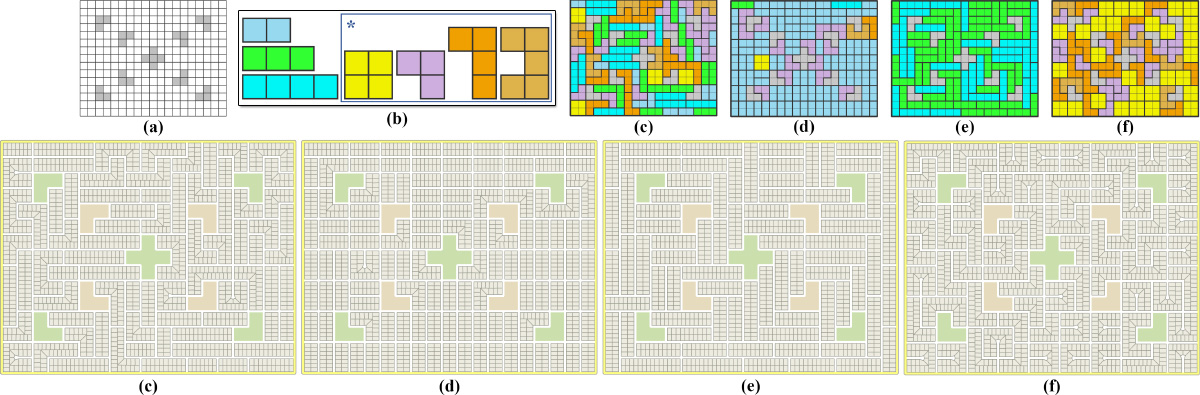
Urban layout design in a regular grid setting. (a) The quadrangulated problem domain. User-specified facility areas are marked in grey. (b) Tile templates. (c) A stochastic-looking design generated using zero weight for the regular-junction constraints and a small randomization factor to perturb the tile placements. (d) A regular-looking design generated using a large weight for the regular-junction constraints; furthermore, each template is constrained to appear at least once (to avoid overly monotonic-looking solutions). (e) A design using templates of longer (3x1 and 4x1) strips only. (f) A design using templates in the marked sub-group only.

(3) Arts and Design

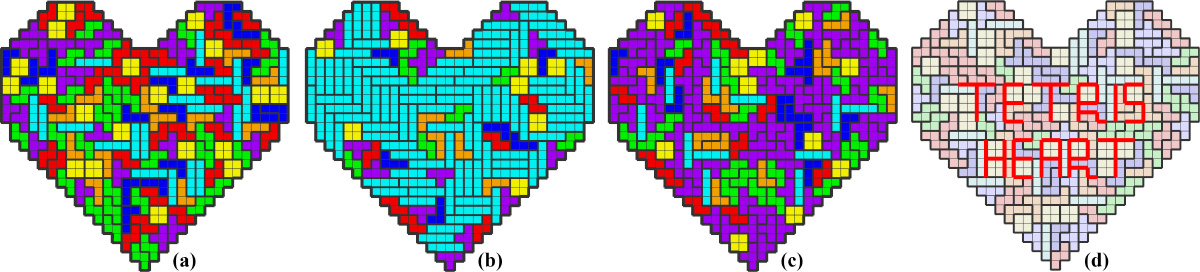
Tetris tiling design with a stochastic distribution by a large randomization factor (a), higher priorities for the 4x1 tiles (b), higher priorities for the T-shaped tiles (c), and with engraved characters imposed by boundary constraints (d).

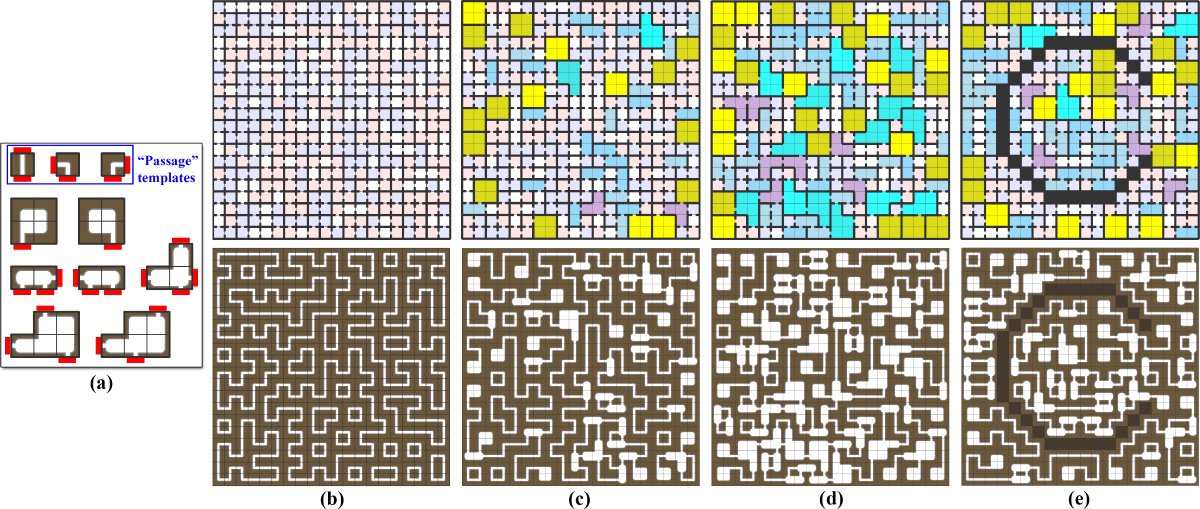
Pattern design using a tile set with edge color constraints to enforce adjacency relationships between tiles. (a) There are two sets of templates: a set of templates presenting caves of predefined sizes and locations of entrances, and a set of single-quad templates to build up the passages, which are allowed to turn arbitrarily, but cannot branch out. Interesting patterns made of caves connected by passages are generated: (b) A design made up of just passages. (c) A design with caves and passages. (d) A design with higher priorities for caves. (e) A design with additional blocking constraints. Note that all the connected components can be easily connected by a post-process, e.g., iteratively digging out an additional passage between two connecting components until all components are singly connected.

---

Acknowledgements

We thank the anonymous reviewers for their insightful comments, Yoshihiro Kobayashi and Christopher Grasso for the renderings, and Virginia Unkefer for the proofreading. This research is supported by the NSF #0643822 and the Visual Computing Center at King Abdullah University of Science and Technology.